Demontração de Huygens (2ª parte)

A fim de provar que a ciclóide é uma curva tautócrona, Huygens considerou a seguinte situação. Tomem-se uma ciclóide e os seguintes pontos:

• O ponto A é o ponto mais baixo da ciclóide.
• O ponto D é o ponto do eixo de simetria da ciclóide que está à mesma altura que os pontos da ciclóide de maior altura.
• Os pontos B e E são pontos da ciclóide, estando B acima de E.
• O ponto F é o ponto onde o eixo de simetria da ciclóide intersecta a recta horizontal que passa por B.
• O ponto Θ é a intersecção da recta horizontal que passa por A com a tangente à ciclóide que passa por B.
• Os pontos G, H e I estão na recta horizontal que passa por E e, além disso,
  
  
  • G está no eixo de simetria da ciclóide,
  • H está na semi-circunferência com extremidades em A e em F, da qual o segmento que une A a F é um diâmetro e com a concavidade voltada para B,
  • I está na tangente à ciclóide que passa por B.

Nestas circunstâncias, Huygens estudou a relação entre dois tempos e dois comprimentos:

t₁:

o tempo que que um objecto leva a deslizar ao longo da ciclóide de B até E, sob a acção da gravidade e partindo da velocidade nula.

t₂:

o tempo que que um objecto leva a deslizar ao longo do declive de B até I, a uma velocidade constante, que seja metade da velocidade que um objecto adquire ao deslizar, sob a acção da gravidade e partindo da velocidade nula, ao longo do declive de B até Θ.

c₁:

comprimento do arco de circunferência que vai de F a H.

c₂:

comprimento do segmento de recta que une F a G.

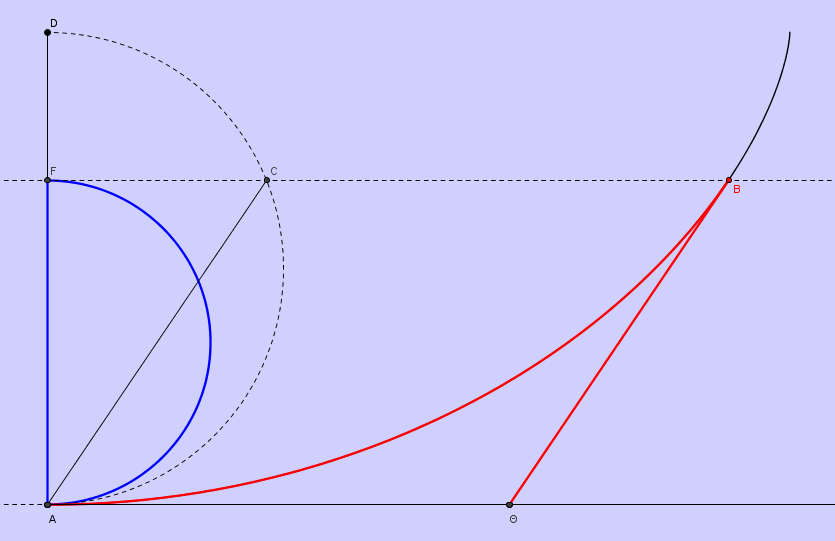
Huygens provou então que ^t₁⁄_t2 = ^c₁⁄_c2. Que a ciclóide é uma curva tautócrona decorre agora do que acontece no caso extremo em que E = A, que é aquele que surge na próxima figura:

Nesta figura também se podem ver a semi-circunferência com extremidades em A e em D, da qual o segmento que une A a D é um diâmetro e com a concavidade voltada para B, o ponto C onde esta semicircunferência intersecta a recta horizontal que passa por B e o segmento que une C a A. Neste caso, ^c₁⁄_c2 é o quociente do comprimento de uma semi-circunferência pelo comprimento do respectivo diâmetro, ou seja, é ^π⁄₂. O tempo t₁ é o tempo que um objecto leva a deslizar, partindo de B à velocidade nula, até chegar ao ponto mais baixo da ciclóide. O tempo t₂ é o tempo que leva um objecto a deslizar ao longo do declive de B até Θ, a uma velocidade constante, que seja metade da velocidade que um objecto adquire ao deslizar, sob a acção da gravidade e partindo da velocidade nula, ao longo do mesmo declive. Huygens provou que este tempo é igual ao tempo que um objecto leva a deslizar de B até Θ sob a acção da gravidade e partindo da velocidade nula. Mas Huygens também provou que o segmento que une B a Θ tem os mesmos declive e comprimento que o que une C a A. E, como já Galileu sabia, o tempo de descida ao longo deste último segmento é igual ao tempo de queda na vertical de D até A.

Próxima secção: Demonstração analítica

Data da última actualização deste documento: 2012–09–28

Autor: José Carlos Santos