Aula nº11

Uso de números aleatórios (continuação)

Vai-se regressar agora aos pontos aleatórios do quadrado que tem por vértices (1,1), (1,-1), (-1,1) e (-1,-1). Dado um tal ponto, como saber se está ou não na circunferência unitária? Basta definir a função

> d:=p->piecewise(p[1]^2+p[2]^2<1,1,0);

e a função

> s:=l->sum(d(l[k]),k=1..nops(l));

Aplicando isto à lista anterior, obtém-se

> s(lista);

Logo, a probabilidade de um ponto daquela lista pertencer à circunferência unitária é igual a

> %/1000.;

Repare-se que a probabilidade de um elemento de uma lista arbitrária pertencer à circunferência unitária é igual a

> evalf(Pi/4);

Cálculo simbólico (continuação)

Considere-se o seguinte problema: uma cabra está amarrada por uma corda a um poste localizado na borda de um terreno circular. Qual deverá ser o comprimento da corda que faz com que a cabra tenha acesso exactamente a metade do terreno? Em termos geométricos, o problema pode ser formulado do seguinte modo: dados dois círculos, com o centro do segundo situado na fronteira do primeiro, qual deverá ser o raio do segundo de modo que a área da intercecção dos círculos seja igual a metade da do primeiro? Como só o quociente dos raios conta, vai-se supor que o primeiro círculo é o círculo unitário do plano e que o segundo tem o centro em (0,-1). Vão-se começar por determinar os pontos de intersecção das fronteiras dos círculos. Para isso, definem-se as funções

> f:=x->-sqrt(1-x^2);

e

> g:=(x,r)->sqrt(r^2-x^2)-1;

Os pontos de intersecção são obtidos resolvendo a equação

> solve(f(x)=g(x,r),x);

É útil definir

> l:=r->[solve(f(x)=g(x,r),x)][1];

Então a área da intersecção das circunferências é dada por

> int(g(x,r)-f(x),x=-l(r)..l(r));

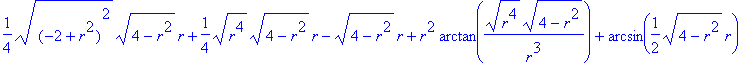
Para se compreender melhor esta expressão, convém simplificá-la. Para tal vai-se supor que r é maior do que 0 e menor do que a raiz quadrada de 2, o que se pode justificar geometricamente.

> assume(0<r,r<sqrt(2));

Então o integral anterior pode ser simplificado fazendo

> simplify(int(g(x,r)-f(x),x=-l(r)..l(r)));

É mesmo possível definir uma função a partir desta expressão fazendo

> h:=unapply(simplify(int(g(x,r)-f(x),x=-l(r)..l(r))),r);

O problema original pode agora ser resolvido fazendo

> fsolve(h(r)=Pi/2,r);

Teoria dos números

Considere-se agora a seguinte função

> t:=n->piecewise(igcd(n,2)=2,n/2,3*n+1);

Note-se que igcd é a função que a dois inteiros associa o seu máximo divisor comum.

Assim, o gráfico de t pode ser visualizado fazendo

> plot([seq([n,t(n)],n=1..30)],style=point,symbol=circle);

Para se ver o gráfico da composta de t consigo própria 6 vezes, pode-se fazer

> plot([seq([n,(t@@6)(n)],n=1..30)],style=point,symbol=circle);